PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set. The algorithm may be applied to any collection of entities with reciprocal quotations and references. The numerical weight that it assigns to any given element E is referred to as the PageRank of E and denoted by PR(E).
The name "PageRank" is a trademark of Google, and the PageRank process has been patented (U.S. Patent 6,285,999). However, the patent is assigned to Stanford University and not to Google. Google has exclusive license rights on the patent from Stanford University. The university received 1.8 million shares of Google in exchange for use of the patent; the shares were sold in 2005 for $336 million
Here’s how it works. If you’ve installed the Google Toolbar, you MAY have the PageRank meter installed. If so, you’ll see it as shown below:
See that big long green bar? That’s the PageRank meter. If you hover over it with your mouse, it will actually show you the PageRank score for the page you are visiting, like this:

Not bad — Google’s home page has a PageRank score of 10! See this part:
(10/10)
That’s Google telling you first the score of the page you’re looking at (10) and the maximum value a page can have overall (10). Google is perfect!
Showing both numbers makes more sense when you get to less perfect pages. Here’s Search Engine Land:

See how we are a 7/10? That means we have a PageRank of 7 out of 10 possible points. Less than perfect. Sniff, sniff. It’s OK. That’s a great score for the home page of a web site that’s only four months old.
Notice how the bar also isn’t all green, in the way it was completely “full” with Google? Instead, like a thermometer, it is only partially filled 7/10ths of the way, to visually represent the page’s PageRank score.
Here’s another page:

Ouch! Zero! This is a terrible page! Actually, no. In this case, I tried to reach a page that doesn’t exist at Search Engine Land. That gave me an error. Since the page doesn’t exist, Google has no PageRank score to report back. That’s why you get a 0 out of 10 score for it. Notice also how the meter has no green, to show no PageRank for the page.
Actual Algorithm
PageRank is a probability distribution used to represent the likelihood that a person randomly clicking on links will arrive at any particular page. PageRank can be calculated for collections of documents of any size. It is assumed in several research papers that the distribution is evenly divided among all documents in the collection at the beginning of the computational process. The PageRank computations require several passes, called "iterations", through the collection to adjust approximate PageRank values to more closely reflect the theoretical true value.
A probability is expressed as a numeric value between 0 and 1. A 0.5 probability is commonly expressed as a "50% chance" of something happening. Hence, a PageRank of 0.5 means there is a 50% chance that a person clicking on a random link will be directed to the document with the 0.5 PageRank.
Simplified algorithm
Assume a small universe of four web pages: A, B, C and D. The initial approximation of PageRank would be evenly divided between these four documents. Hence, each document would begin with an estimated PageRank of 0.25.
In the original form of PageRank initial values were simply 1. This meant that the sum of all pages was the total number of pages on the web at that time. Later versions of PageRank (see the formulas below) would assume a probability distribution between 0 and 1. Here a simple probability distribution will be used—hence the initial value of 0.25.
If pages B, C, and D each only link to A, they would each confer 0.25 PageRank to A. All PageRank PR( ) in this simplistic system would thus gather to A because all links would be pointing to A.
This is 0.75.
Suppose that page B has a link to page C as well as to page A, while page D has links to all three pages. The value of the link-votes is divided among all the outbound links on a page. Thus, page B gives a vote worth 0.125 to page A and a vote worth 0.125 to page C. Only one third of D's PageRank is counted for A's PageRank (approximately 0.083).
In other words, the PageRank conferred by an outbound link is equal to the document's own PageRank score divided by the normalized number of outbound links L( ) (it is assumed that links to specific URLs only count once per document).
In the general case, the PageRank value for any page u can be expressed as:
 ,
,
i.e. the PageRank value for a page u is dependent on the PageRank values for each page v out of the set Bu (this set contains all pages linking to page u), divided by the number L(v) of links from page v.
Damping factor The PageRank theory holds that even an imaginary surfer who is randomly clicking on links will eventually stop clicking. The probability, at any step, that the person will continue is a damping factor d. Various studies have tested different damping factors, but it is generally assumed that the damping factor will be set around 0.85.The damping factor is subtracted from 1 (and in some variations of the algorithm, the result is divided by the number of documents ( N ) in the collection) and this term is then added to the product of the damping factor and the sum of the incoming PageRank scores. That is,
So any page's PageRank is derived in large part from the PageRanks of other pages. The damping factor adjusts the derived value downward. The original paper, however, gave the following formula, which has led to some confusion:
The difference between them is that the PageRank values in the first formula sum to one, while in the second formula each PageRank gets multiplied by N and the sum becomes N. A statement in Page and Brin's paper that "the sum of all PageRanks is one" and claims by other Google employees support the first variant of the formula above.
To be more specific, in the latter formula, the probability for the random surfer reaching a page is weighted by the total number of web pages. So, in this version PageRank is an expected value for the random surfer visiting a page, when he restarts this procedure as often as the web has pages. If the web had 100 pages and a page had a PageRank value of 2, the random surfer would reach that page in an average twice if he restarts 100 times. Basically, the two formulas do not differ fundamentally from each other. A PageRank that has been calculated by using the former formula has to be multiplied by the total number of web pages to get the according PageRank that would have been calculated by using the latter formula. Even Page and Brin mixed up the two formulas in their most popular paper "The Anatomy of a Large-Scale Hypertextual Web Search Engine", where they claim the latter formula to form a probability distribution over web pages with the sum of all pages' PageRanks being one.
Google recalculates PageRank scores each time it crawls the Web and rebuilds its index. As Google increases the number of documents in its collection, the initial approximation of PageRank decreases for all documents.
The formula uses a model of a random surfer who gets bored after several clicks and switches to a random page. The PageRank value of a page reflects the chance that the random surfer will land on that page by clicking on a link. It can be understood as a Markov chain in which the states are pages, and the transitions are all equally probable and are the links between pages.
If a page has no links to other pages, it becomes a sink and therefore terminates the random surfing process. If the random surfer arrives at a sink page, it picks another URL at random and continues surfing again.
When calculating PageRank, pages with no outbound links are assumed to link out to all other pages in the collection. Their PageRank scores are therefore divided evenly among all other pages. In other words, to be fair with pages that are not sinks, these random transitions are added to all nodes in the Web, with a residual probability of usually d = 0.85, estimated from the frequency that an average surfer uses his or her browser's bookmark feature.
So, the equation is as follows:
where p1,p2,...,pN are the pages under consideration, M(pi) is the set of pages that link to pi, L(pj) is the number of outbound links on pagepj, and N is the total number of pages.
The PageRank values are the entries of the dominant eigenvector of the modified adjacency matrix. This makes PageRank a particularly elegant metric: the eigenvector is
where R is the solution of the equation
where the adjacency function  is 0 if page pj does not link to pi, and normalized such that, for each j
is 0 if page pj does not link to pi, and normalized such that, for each j
 is 0 if page pj does not link to pi, and normalized such that, for each j
is 0 if page pj does not link to pi, and normalized such that, for each j ,
,
The facts that we do know about page rank are;
1. One-way inbound links from websites with topics that are related to your website's topic will help you gain a higher page rank.
2. Other one-way inbound links from pages with high page rank but unrelated topics do help a little, but not nearly as much.
3. The number of links outbound from the website that links to you also determines the value of the link. A related website with 10 outbound links that links to you is much better than a related website with 100 outbound links that link to you.
The website I referred to above loves to state a lot of things as fact, such as,
"Fact: A website has a maximum amount of PageRank that is distributed between its pages by internal links.
The maximum PageRank in a site equals the number of pages in the site * 1. The maximum is increased by inbound links from other sites and decreased by outbound links to other sites. We are talking about the overall PageRank in the site and not the PageRank of any individual page. You don't have to take my word for it. You can reach the same conclusion by using a pencil and paper and the equation.
Fact: The maximum amount of PageRank in a site increases as the number of pages in the site increases.
The more pages that a site has, the more PageRank it has. Again, by using a pencil and paper and the equation, you can come to the same conclusion. Bear in mind that the only pages that count are the ones that Google knows about.
I dispute both of those "facts". I cannot get a page rank of 30,000 in my article directory although I have 30,000 pages in it that have been indexed by google. Again, an elementary conclusion.
There are seo gurus who will tell you that the higher the page rank the deeper Google will crawl your website. Maybe. Google doesn't say that is the case though.
Also important to keep in mind that search engines crawl and index webpages not websites, that is why your page rank may vary from page to page within your website.
Good internal linking and navigation can help distribute page rank well throughout your website. Your index page is the most important page Google indexes and your other pages will inherit some page rank from your index page because it is linked from there.
I have one website that is a PR4 on the main page but contains several PR5 and PR6 webpages in the interior of the website proving that Google ranks webpages individually.
When you are doing your link building campaign, do it for more than just the index page. Put links out there for your interior pages as well.
Webmasters and individuals will link to quality content and quality content is the single best way to higher page rank and search engine listings. Content is still king. Links are not king.
People link to articles and content that is original and well-written and that contain quality information not found elsewhere. Google also ranks webpages higher in listings that have quality content. That’s why it is still the best SEO method there is.
Soon we will post on tips related to how to increase your page rank of our website, so keep coming back..





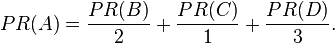




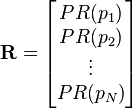
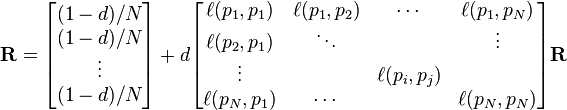











0 comments:
Post a Comment